Butterworth Low Pass Filter merupakan filter yang memiliki respon frekuensi maksimum datar (tidak ada ripple) dari frekuensi 0 Hz hingga akhir daerah pass band yaitu frekuensi cut off yang mengalami pelemahan -3dB.
Low Pass Filter Pasif Orde 1
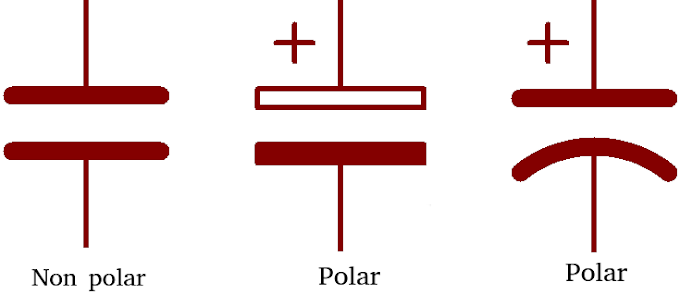
Gambar 1 menunjukan dasar rangkaian low pass filter pasif menggunakan komponen Resistor (R) dan kapasitor (C).
 |
| Gambar 1. Rangkaian dasar Low Pass Filter pasif orde 1 |
Saat frekuensi rendah, kapasitor diasumsikan open atau tidak terhubung dan tidak ada redaman sinyal karena Voutput = Vinput. Persamaan pada rangkaian low pass filter pasif Gambar 1 adalah :

dimana besarnya XC dapat dihitung menggunakan persamaan :

jika jω = s maka XC dapat ditulis menjadi :
Untuk mencari nilai frekuensi cut off dapat dicari dengan persamaan :

Low Pass Filter Pasif Orde 2











Gambar 2 menunjukan dasar rangkaian low pass filter orde 2 menggunakan komponen dasar resistor dan kapasitor.
 |
| Gambar 2. Rangkaian dasar low pass filter pasif orde 2 |
Rangkaian dasar low pass filter pasif orde 2 pada Gambar 2 memiliki beberapa persamaan sebagai berikut :


Jika nilai komponen dibuat sama yaitu C1 = C2 = C dan R1 = R2 = R maka persamaan di atas dapat ditulis sebagai berikut:


Jika Anda membandingkan persamaan di atas dengan transfer function low pass filter orde 2 memiliki bentuk yang mirip. Berikut adalah transfer function umum dari low pass filter orde 2.

Dari perbandingan bentuk transfer function low pass filter dengan persamaan filter orde 2 di atas dapat dicari nilai ω0 sebagai berikut :


ω0 merupakan frekuensi sudut saat frekuensi cut off sehingga ω0 = ωc = 2.π.fC.C maka :

Karena nilai komponen dibuat sama yaitu C1 = C2 = C dan R1 = R2 = R sehingga masing-masing blok memiliki frekuensi cut off sama sehingga persamaan untuk mencari frekuensi cut off menjadi :

Dengan menggunakan nilai C sama dan R sama maka transfer function untuk low pass filter orde 2 rangkaian LPF Gambar 2 dapat ditulis menjadi :

dimana :
k = gain atau penguatan
ωC = frekuensi sudut cut off
Untuk mencari nilai faktor Q filter dapat menggunakan transfer function dan persamaan yang dibahas sebelumnya sebagai berikut :

Nilai Q menggambarkan nilai puncak (peak) pada titik frekuensi cut off. Dalam mendesain filter Butterworth memiliki nilai Q maksimum 0,707 yang menyebabkan respon frekuensi tanpa ripple.
Saat kita meng-cascade rangkaian filter orde 1 menjadi orde 2 seperti ditunjukan Gambar 2, maka frekuensi cut off bergeser sehingga tidak memungkinkan mendesain filter pasif dengan orde lebih dari 1. Untuk membuat filter orde tinggi (lebih dari 1) maka perlu menggunakan komponen aktif atau mendesain aktif filter.
Untuk mendesain filter Butterworth diperlukan Q hingga 0,707, untuk mencapai hal ini diperlukan paling tidak ada 1 positif feedback atau umpan balik dan hal ini hanya dimungkinkan jika kita menggunakan komponen aktif (aktif filter).
Kesimpulan : Filter pasif hanya cocok digunakan untuk orde 1, jika lebih dari 1 tidak cocok karena Q rendah yaitu 0,5 selain itu saat di-cascade frekuensi cut off dapat bergeser.
Low Pass Filter Aktif Orde 1
Low pass filter aktif orde 1 dapat dibangun dari pasif low pass filter orde 1 yang ditambahkan komponen op-amp seperti ditunjukan pada Gambar 3.
 |
| Gambar 3. Low Pass Filter aktif orde 1 |
Gambar 3a menunjukan rangkaian dasar low pass filter aktif tanpa penguatan atau lebih umum disebut dengan unity gain, sedangkan Gambar 3b menunjukan rangkaian low pass filter aktif menggunakan penguatan yang besarnya tergantung dari nilai R2 dan R3.
Dengan filter aktif Anda dapat meng-cascade rangkaian filter untuk mendapatkan orde lebih tinggi tanpa terjadi pergeseran frekuensi cut off serta memperoleh Q lebih besar karena memiliki penguatan op-amp. Persamaan filter pasif orde 1 dan orde 2 dapat digunakan pada filter aktif.
Penguatan op-amp pada rangkaian filter Gambar 3b dapat dicari menggunakan persamaan :

Untuk mencari besarnya frekuensi cut off rangkaian filter pada Gambar 3 adalah dengan persamaan :

Filter aktif orde 1 memiliki respon frekuensi dengan kemiringan kurva -6 dB per oktav atau -20 dB per Dekade.
Low Pass Filter Aktif Orde 2
Low Pass Filter aktif orde 2 memiliki gambar respon frekuensi sama seperti low pass filter orde 1 yang ditunjukan oleh Gambar 4. Hal yang membedakan adalah pada orde 1 memiliki kecuraman atau kemiringan kurva -20dB per dekade, sedang filter orde 2 memiliki kecuraman -40dB per dekade.
 |
| Gambar 4. Respon frekuensi Low Pass Filter orde 2 |
Sallen-Key filter adalah topologi filter orde 2 yang digunakan sebagai dasar untuk membangun filter orde lebih tinggi seperti membangun rangkain filter orde 2, orde 3 dan seterusnya. Topologi Sallen - Key merupakan filter aktif menggunakan satu op-amp dengan penguatan non-inverting dan menggunakan total empat komponen pasif (dua kapasitor dan dua resistor).
Filter aktif orde 2 memiliki dua tahap filter yang umumnya terdiri dari dua komponen aktif dimana masing-masing komponen aktif memiliki satu resistor dan satu kapasitor atau hanya memiliki satu komponen aktif dan memiliki dua kapasitor dan dua resistor yang bertujuan untuk mendapatkan respon kemiringan kurva lebih baik yaitu -40dB per dekade.
Dalam membangun filter dengan orde n dimana n lebih tinggi dari 2, maka filter tersebut dapat dibangun menggunakan kombinasi filter orde 2 dan orde 1 yang disusun secara berurutan seperti ditunjukan pada Gambar 5.
 |
| Gambar 5. Diagram desain Low Pass Filter aktif orde n |
Untuk mempermudah dalam mendesain Butterworth low pass filter diberikan Tabel 1 yaitu faktor polinomial Butterworth orde 1 dan orde 2.
Tabel 1. Faktor Polinomial


Rangkaian Sallen-Key filter low pass filter tanpa penguatan atau biasa disebut unity gain ditunjukan oleh Gambar 6.
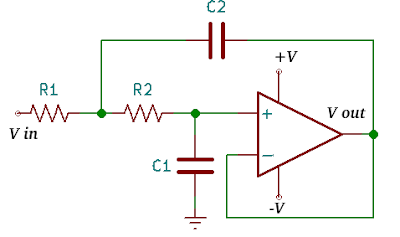 |
| Gambar 6. Sallen-Key Low Pass Filter unity gain |
Gambar 7 menunjukan rangakain Sallen-Key filter menggunakan penguatan dimana besarnya penguatan tergantung dari nilai R3 dan R4.
 |
| Gambar 7. Sallen-Key Low Pass Filter dengan penguatan |
Dimana :
k adalah penguatan atau gain dan umumnya ditulis A0. Jika R1 = R2 = R dan C1 = C2 = C, maka transfer function Sallen Key low pass filter menjadi :

Jika Anda membandingkan transfer function Sallen-Key dengan transfer function low pass filter orde 2 maka didapatkan beberapa persamaan yaitu :

Faktor kualitas Q dipengaruhi oleh k dimana k umumnya ditulis A0 sehingga:

Frekuensi cut off atau frekuensi resonansi : 

Penguatan Op-amp (Gambar 7) dapat dituliskan : 

Q atau faktor kualitas menggambarkan respon puncak saat pada titik frekuensi cut off atau frekuensi resonansi, yaitu daerah tinggi dan sempit disekitar frekuensi cut off. Nilai Q pada filter orde n dapat dicari dengan mengacu pada faktor polinomial Butterworth yang ditunjukan pada Tabel 1.
Butterworth Low Pass Filter
Butterworth filter memiliki respon pass band flat atau datar (tidak ada ripple) hingga frekuensi mencapai cut off dan memiliki kemiringan kurva yang linier karena memiliki nilai Q = 0,707. Gambar 8 menunjukan kurva respon frekuensi filter Butterworth.
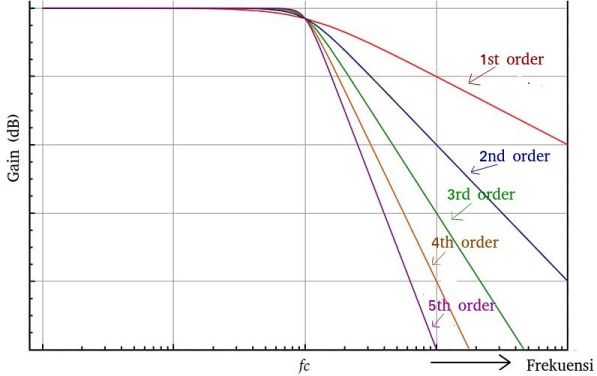 |
| Gambar 8. Respon frekuensi Butterworth Low Pass Filter |
Untuk mengetahui orde n filter Butterworth yang akan dirancang dapat dicari dengan persamaan :


Keterangan :
H: Besarnya pelemahan filter.
fs : Frekuensi saat stop band.
fp : Frekuensi saat passband.
n : Orde filter.
ε (epsilon) : Maksimum penguatan pass band (frekuensi yang diloloskan). Jika penguatan didesain pada titik -3dB frekuensi cut off, ε akan sama dengan 1. Jika menginginkan penguatan nilai lain maka nilai epsilon (ε) dapat dicari dengan persamaan di bawah :

Keterangan :
H0 = Penguatan maksimum pada pass band.
H1 = Penguatan minimum (pelemahan) pada pass band.
Jika Anda menginginkan filter dengan orde tinggi karena ingin mendapatkan kecuraman kurva lebih Anda dapat membangun filter menggunakan orde 1 dan orde 2 yang disusun secara berurutan. Contoh jika Anda menginginkan low pass filter orde 3 maka Anda membutuhkan satu filter orde 1 dan filter orde 2 dimana akan memiliki kecuraman filter = -20dB -20dB -20dB / Dekade = -60dB/Dekade atau kecuraman -6dB -6dB -6dB = -18dB/Oktav.
Contoh 1: Mendesain low pass filter Butterworth :
Filter Butterworth mempunyai spesifikasi penguatan maksimum adalah 0,5 dB pada daerah frekuensi pass band 40 Hz dan pelemahan sebesar -20 dB saat frekuensi daerah stop band 130 Hz. Buat rangkaian filter Butterworth tersebut.
Jawab :0,5 dB = 20 log (A max) -> Amax = 1,0593
-20 dB = 20 log (A min) -> Amin = 1/10 (mengalami pelemahan 10 x) saat stop band.
Pass band : 40 Hz.
Stop band : 130 Hz.
Langkah pertama - Mencari epsilon saat penguatan maksimum



Langkah kedua - Mencari orde n filter yang akan dirancang dimana mengalami pelemahan 10x :








Dari hasil perhitungan orde n dapat disimpulkan bahwa untuk memenuhi spesifikasi yang diminta perlu dibuat Butterworth filter orde 3 yang memerlukan satu filter Butterworth orde 1 dan satu Butterworth orde 2 yang disusun secacara berurutan.
Langkah ketiga : Mencari nilai faktor Q filter orde 3.
Dari data pada Tabel 1, filter orde 3 memiliki faktor polinomial (1 + s) (s 2 + s + 1) yang membantu untuk menentukan nilai Q dengan membandingkan bentuk transfer function low pass filter orde 2 yang menghasilkan Q orde 2 sama dengan 1.

Q = 1 / (3-A0)
1= 1 / (3 - A0)
3-A0 = 1
A0 = 2
Langkah keempat - Menentukan nilai resistor penguatan dengan menentukan nilai satu resistor dengan sembarang nilai yang ada dipasaran, contoh R3 diberi nilai 1k. sehingga resistor penguatan lainnya dapat dicari sbb :
A0 = (R3/R4) + 1
2 = (1k / R4) +1 1 = 1k / R4
R4 = 1k
Langkah kelima - Mencari frekuensi cut off yang ditandai dengan pelemahan -3dB pada titik frekuensi cut off, menggunakan rumus yang digunakan untuk mencari orde n filter sebagai berikut :

Dimana ωc = frekuensi sudut saat cut off = 2.π.fC
Dimana ωp = frekuensi sudut saat stop band = 2.π.fp
Sehingga untuk mencari frekuensi cut off adalah dengan memberi nilai H = -3dB karena karakteristik saat berada pada frekuensi cut off sinyal mengalami pelemahan sebesar -3dB :








Dari hasil perhitungan di atas didapatkan besarnya frekuensi cut off filter orde 3 adalah 56,79 Hz.
Langkah keenam - Mencari nilai R dan C rangkaian filter.
Setelah mengetahui nilai frekuensi cut off, dapat dicari nilai R dan C rangkaian filter dengan rumus umum :
fc = 1 / (2π.R.C), tentukan satu nilai C untuk mendapatkan nilai R atau sebaliknya, diambil contoh nilai C 1uF maka nilai R adalah sbb :
R = 1 / (2π.fC.C)
R = 1 / (2. 3,14. 56,79. 1uF)
R = 2,8 k
Langkah ketujuh - Manggambar rangkaian Butterworth low pass filter orde 3.
Dari perhitungan besarnya C dan R didapatkan gambar rangkaian low pass filter Butterworth orde 3 ditunjukan pada Gambar 6 dimana rangkaian dibangun dari dua rangkaian filter yaitu : satu rangkaian LPF orde 2 dan satu rangkaian LPF orde 1.
 |
| Gambar 9. Rangkaian low pass filter Butterworth orde 3 |
Contoh 2: Mendesain filter Butterworth low pass filter orde 2 dengan frekuensi cut off 1kHz.
Jawab :
Untuk menentukan nilai R perlu memberi nilai C sembarang nilai atau sebaliknya, diambil contoh nilai resistor sebesar 4,7k.
C = 1 / (2.π.fC.R) C = 1 / (2 . 3,14 . 1000. 4700)
C = 33,9 nF
Untuk mencari penguatan filter berpatokan nilai Q Butterworth dimana orde 2 memiliki faktor polinomial (s2 + 1,414s + 1).

A0 = 3 - (1 / Q)
A0 = 3 - (1 / 0,707)
A0 = 1,585
Mencari nilai R untuk penguatan dengan memberikan satu nilai R sembarang nilai diambil, contoh R3 2,2k maka :
A0 = R3/ R4 + 1
A0 - 1 = R3/ R4
1,585 - 1 = 2,2 k / R4
R4 = 2,2k / 0,585
R4 = 3,8k
Dari perhitungan di atas didapatkan gambar filter Butterworth yang ditunjukan pada Gambar 10.
 |
| Gambar10. Rangkaian filter Butterworth orde 2 |
EoF