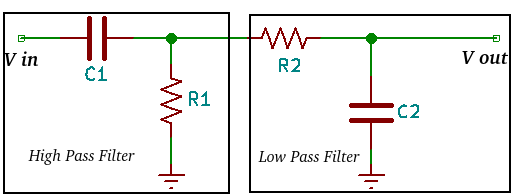
Butterworth High Pass Filter merupakan filter yang meloloskan frekuensi tinggi dan memiliki respon frekuensi maksimum datar (tidak ada ripple) dari frekuensi cut off dengan redaman -3dB hingga daerah pass band tanpa redaman.
High Pass Filter Pasif Orde 1
High pass filter pasif orde 1 adalah filter menggunakan komponen satu kapasitor dan satu resistor yang disusun sedemikian rupa seperti ditunjukan pada Gambar 1.
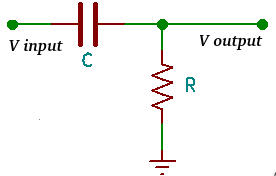 |
| Gambar 1. High Pass Filter pasif orde 1 |
Persamaan yang berhubungan dengan high pass filter pasif adalah sbb :
Besarnya frekuensi cut off (fC) filter adalah :

Perbandingan Voutput dan Vinput adalah sbb :



High Pass Filter Pasif Orde 2
High pass filter orde 2 dibangung dengan meng-cascade high pass filter orde1 secara berurutan seperti ditunjukan pada Gambar 2.
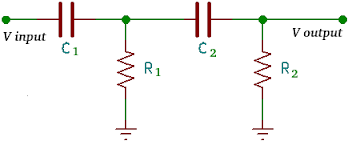 |
| Gambar 2. High pass filter pasif orde 2 |
Persamaan Gambar 2 di atas dapat ditulis sebagai berikut :


Jika nilai nilai resistor dibuat sama yaitu R1 = R2 = R dan nilai kapasitor dibuat sama yaitu C1 = C2 = C maka transfer function menjadi :


Filter pasif Gambar 2 sulit diimplementasikan jika ingin memiliki filter lebih dari orde 1 karena impedansi input mempengaruhi impedansi output sehingga frekuensi cut off akan selalu bergeser dari perhitungan.
Untuk membangun high pass filter lebih tinggi dari orde 2 dapat dibangun menggunakan dasar high pass filter orde 1 dan high pass filter orde 2 yang disusun secara berurutan atau cascade seperti ditunjukan pada Gambar 3.
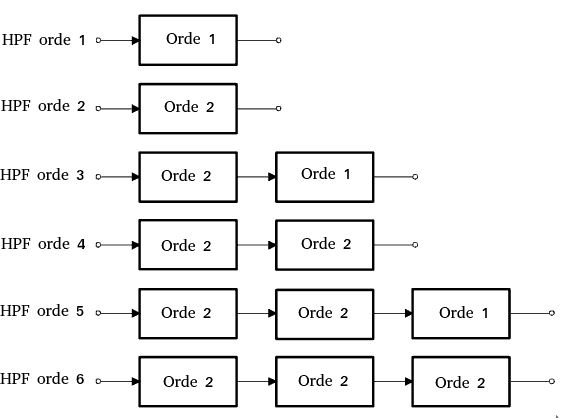 |
| Gambar 3. Membangun High Pass Filter orde n |
High Pass Filter Aktif Orde 1
Gambar 4 menunjukan rangkaian dasar high pass filter orde 1 non inverting yang memiliki kurva respon frekuensi dengan kecuraman atau kemiringan kurva -6dB per oktav atau -20dB per Dekade saat frekuensi di bawah frekuensi cut off seperti ditunjukan pada Gambar 5.
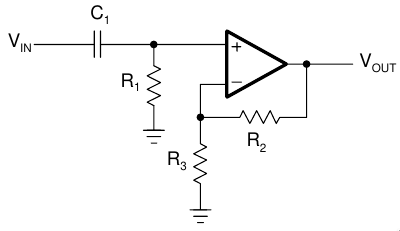 |
| Gambar 4. Rangkaian high pass filter orde 1 |
High Pass Filter Aktif Orde 2
High pass filter orde 2 memiliki kecuraman kurva sebesar -12 dB / oktav atau kecuraman -40dB/Dekade. Gambar 5 menunjukan perbandingan respon frekuensi high pass filter orde 1 dan orde 2 dimana masing-masing filter memiliki kesamaan pelemahan sebesar -3 dB saat frekuensi cut off, yang membedakan keduanya adalah kemiringan atau kecuraman kurva.
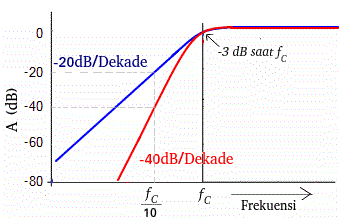 |
| Gambar 5. Kurva respon frekuensi High Pass Filter |
High Pass Filter orde 2 pada bahasan ini adalah menggunakan topologi Sallen Key seperti ditunjukan pada Gambar 6.
 |
| Gambar 6. Topologi Sallen Key High Pass Filter |
Sallen Key high pass filter Butterworth memiliki nilai kualitas Q sama seperti low pass filter Butterworth yaitu sebesar 0,707, dan hal ini menyebabkan respon filter pada titik frekuensi cut off hingga frekuensi pass band rata atau tidak ada riak (ripple).
Rangkaian Sallen-Key High Pass Filter Gambar 6 memiliki transfer function sebagai berikut :

Jika nilai R1 = R2 = R, dan C1 = C2 = C, lalu ωc = 1 / (RC) maka transfer function Sallen Key pada menjadi :


Jika membandingkan transfer function rangakain Sallen Key dengan transfer function high pass filter orde 2 akan didapatkan beberapa persamaan sebagai berikut :

k umumnya ditulis menjadi A0 sehingga besarnya Q dapat dihitung dengan persamaan : 

Untuk mencari nilai frekuensi resonansi atau frekuensi cut off Sallen Key high pass filter dimana R1 = R2 = R, dan C1 = C2 = C menggunakan persamaan sebagai berikut : 

Besarnya penguatan op-amp dapat dicari dengan persamaan : 

Gambar 7 menunjukan susunan rangkaian high pass filter orde n dimanan jika nilai n lebih dari 2 maka rangkaian filter merupakan gabungan susunan filter orde 1 dan orde 2. Contoh : High pass filter orde 4 dibangun menggunakan 2 buah high pass filter orde 2.
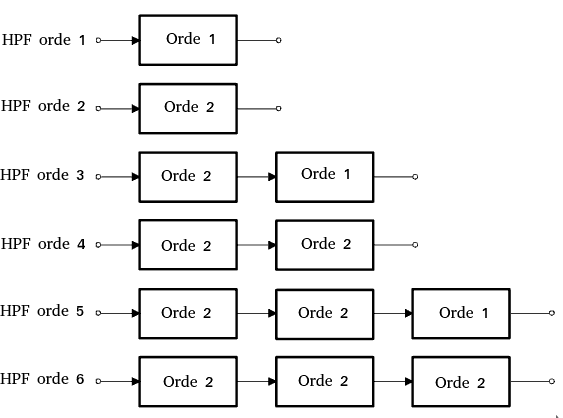 |
| Gambar 7. Desain High pass filter orde n |
Untuk mempermudah dalam mendesain high pass filter orde n dapat menggunakan tabel Polinomial high pass filter yang ditunjukan pada Tabel 1.

Untuk mencari besarnya orde n high pass filter Butterworth dapat menggunakan persamaan :


Langkah ketiga : Mencari penguatan masing-masing rangkaian filter Butterworth orde 2.
Rangkaian filter 1 :
Q = 1 / (3-A0)
1,451 = 1 / (3-A0)
3-A0 = 1 / 1,451
3-A0 = 0,69
A0 = 2,31
Kemudian beri nilai salah satu resistor untuk penguatan opamp dengan sembarang nilai contoh R3 = 1k maka R4 dapat dicari sebagai berikut :
A0 = (R3 / R4) + 1
2,31 = (1k / R4) + 1
0,31 = 1k / R4
R4 = 1k / 0,31
R4 = 3,2 k
Rangkaian filter 2 :
Q = 1 / (3-A1)
0,54 = 1 / (3-A1)
3-A1 = 1 / 0,54
3-A1 = 1,852
A1 = 1,15
Kemudian beri nilai pada salah satu resistor untuk penguatan op-amp, contoh R7 = 1k maka R8 dapat dicari sebagai berikut :
A1 = (R7 / R8) + 1
1,15 = (1k / R8) + 1
0,15 = 1k / R8
R8 =1k / 0,15
R8=6,67k
Langkah keempat : Mendesain rangkaian high pass filter orde 4 yang ditunjukan pada Gambar 9.
Tabel 1. Faktor Polinomial High Pass Filter

Untuk mencari besarnya orde n high pass filter Butterworth dapat menggunakan persamaan :


Keterangan :
H = Pelemahan atau redaman saat frekuensi cut off
n = orde filter
ε (epsilon) = Maksimum penguatan pass band (frekuensi yang diloloskan). Jika penguatan didesain pada titik -3dB frekuensi cut off (fc), ε akan sama dengan 1 dan ε2 juga sama dengan 1. Jika menginginkan penguatan nilai lain maka nilai epsilon (ε) dapat dicari dengan persamaan di bawah : 

Keterangan :
H0 = Penguatan maksimum pada pass band.
H1 = Penguatan minimum (pelemahan) pada pass band.
Contoh soal 1:
Butterworth high pass filter memiliki spesifikasi penguatan maksimum 0,5 dB pada daerah pass band 130 Hz dan pelemahan atau redaman sebesar -20dB pada frekuensi stop band 40 Hz. Desain high pass filter Butterworth dan Gambar rangkaiannya.
Jawab :
Diketahui :
0,5 dB = 20 log (Amax) -> Amax = 1,0593
-20 dB = 20 log (Amin) -> Amin = 1 / 10 (mengalami pelemahan 10x) pada posisi stop band.
Pass band : 130 Hz
Stop band : 40 Hz
Langkah pertama : Mencari epsilon saat penguatan maksimum
H0 / H1 = √ (ε 2+ 1)
(1,0593 ) 2= ε + 1
ε 2= 0,1221
ε = 0,3494
Langkah kedua : Mencari orde n high pass filter dari variabel, diketahui pelemahan dimana -20 dB saat stop band 40 Hz.









Sehingga nilai Q = 0,707
Langkah keempat : Menentukan nilai R3 dan R4 untuk penguatan op-amp.
Dari nilai Q yang didapatkan dapat digunakan untuk mencari nilai R3 dan R4 dengan cara menentukan salah satu nilai R acak, diambil contoh R3 = 1k, maka R4 dapat dicari sebagai berikut :
Q = 1 / (3-A0)
0,707 = 1 / (3-A0)
3-A0 = 1,414
A0 = 1,58
A0 = (R3 / R4) + 1
1,58 = 1 / R4 + 1
R4 = 1k / 0,58
R4 = 1,72k
Langkah kelima : Mencari frekuensi cut off yang ditandai terjadi pelemahan sebesar -3dB dengan persamaan :









Langkah ketujuh : Menggambar rangkaian high pass filter Butterworth orde 3.
Contoh soal 2:
Desain rangkaian Butterworth high pass filter orde 4 dengan frekuensi cut off 1KHz.
Untuk menjawaba soal 2 di atas perlu beberapa langkah :
Langkah pertama: Menentukan nilai R dan C rangkaian filter dengan menentukan salah satu nilai komponen, contoh R = 4,7k, maka C dapat dicari sebagai berikut :
fc = 1 / ( 2 . π . R . C )
C = 1 / ( 2 . π . fc .R )
C = 1 / ( 2 . 3,14 . 1000. 4700 )
C = 33,9 nF
Langkah kedua : Mencari nilai Q filter.
High pass filter orde 4 dibangun dari dua rangkaian filter orde 2 sehingga masing masing rangkaian memiliki Q sendiri dimana nilainya dapat dilihat dari faktor polinomial high pass filter orde 4 yaitu : dengan membandingkan bentuk (s2 + 0,7065s + 1) (s2 + 1,848s + 1) dengan transfer function umum orde 2 high pass filter, sehingga :
Contoh soal 1:
Butterworth high pass filter memiliki spesifikasi penguatan maksimum 0,5 dB pada daerah pass band 130 Hz dan pelemahan atau redaman sebesar -20dB pada frekuensi stop band 40 Hz. Desain high pass filter Butterworth dan Gambar rangkaiannya.
Jawab :
Diketahui :
0,5 dB = 20 log (Amax) -> Amax = 1,0593
-20 dB = 20 log (Amin) -> Amin = 1 / 10 (mengalami pelemahan 10x) pada posisi stop band.
Pass band : 130 Hz
Stop band : 40 Hz
Langkah pertama : Mencari epsilon saat penguatan maksimum
H0 / H1 = √ (ε 2+ 1)
(1,0593 ) 2= ε + 1
ε 2= 0,1221
ε = 0,3494
Langkah kedua : Mencari orde n high pass filter dari variabel, diketahui pelemahan dimana -20 dB saat stop band 40 Hz.









Dari perhitungan di atas didapatkan orde n high pass filter adalah 2,83 dibulatkan menjadi n = 3.
Langkah ketiga: mencari nilai faktor Q high pass filter orde 3.
Dari data Tabel 1 menunjukan filter orde 3 memiliki faktor polinomial (1 + s) (s 2 + s + 1) yang dapat membantu mendapatkan nilai Q dengan membandingkannya dengan transfer function Sallen Key filter orde 2 karena orde 3 dibangun dari orde 2 ditambah dengan orde 1.

Langkah keempat : Menentukan nilai R3 dan R4 untuk penguatan op-amp.
Dari nilai Q yang didapatkan dapat digunakan untuk mencari nilai R3 dan R4 dengan cara menentukan salah satu nilai R acak, diambil contoh R3 = 1k, maka R4 dapat dicari sebagai berikut :
Q = 1 / (3-A0)
0,707 = 1 / (3-A0)
3-A0 = 1,414
A0 = 1,58
A0 = (R3 / R4) + 1
1,58 = 1 / R4 + 1
R4 = 1k / 0,58
R4 = 1,72k
Langkah kelima : Mencari frekuensi cut off yang ditandai terjadi pelemahan sebesar -3dB dengan persamaan :

fc : Frekuensi cut off.
fp : Frekuensi pass band.
H = -3dB (syarat frekuensi cut off selalu di -3dB)









Sehingga frekuensi cut off terjadi pada frekuensi 91,56 Hz.
Langkah keenam : Mencari nilai R dan C
Mencari nilai C atau R dengan menentukan sembarang nilai pada salah satu komponen, contoh diambil nilai C = 100nF.
fc = 1 / ( 2π R C )
R = 1 / ( 2π fc C )
R = 1 / ( 2 . 3,14 . 91,56 . 100nF )
R = 17,4 k
Dari semua nilai hasil perhitungan di atas desain gambar rangkaian Butterwworth high pass filter orde 3 ditunjukan pada Gambar 8.
 |
| Gambar 8. Rangkaian Butterworth high pass filter aktif orde 3 |
Desain rangkaian Butterworth high pass filter orde 4 dengan frekuensi cut off 1KHz.
Untuk menjawaba soal 2 di atas perlu beberapa langkah :
Langkah pertama: Menentukan nilai R dan C rangkaian filter dengan menentukan salah satu nilai komponen, contoh R = 4,7k, maka C dapat dicari sebagai berikut :
fc = 1 / ( 2 . π . R . C )
C = 1 / ( 2 . π . fc .R )
C = 1 / ( 2 . 3,14 . 1000. 4700 )
C = 33,9 nF
Langkah kedua : Mencari nilai Q filter.
High pass filter orde 4 dibangun dari dua rangkaian filter orde 2 sehingga masing masing rangkaian memiliki Q sendiri dimana nilainya dapat dilihat dari faktor polinomial high pass filter orde 4 yaitu : dengan membandingkan bentuk (s2 + 0,7065s + 1) (s2 + 1,848s + 1) dengan transfer function umum orde 2 high pass filter, sehingga :

Jadi Q rangkaian filter 1 = 1,415 dan Q rangkaian filter 2 = 0,54
Langkah ketiga : Mencari penguatan masing-masing rangkaian filter Butterworth orde 2.
Rangkaian filter 1 :
Q = 1 / (3-A0)
1,451 = 1 / (3-A0)
3-A0 = 1 / 1,451
3-A0 = 0,69
A0 = 2,31
Kemudian beri nilai salah satu resistor untuk penguatan opamp dengan sembarang nilai contoh R3 = 1k maka R4 dapat dicari sebagai berikut :
A0 = (R3 / R4) + 1
2,31 = (1k / R4) + 1
0,31 = 1k / R4
R4 = 1k / 0,31
R4 = 3,2 k
Rangkaian filter 2 :
Q = 1 / (3-A1)
0,54 = 1 / (3-A1)
3-A1 = 1 / 0,54
3-A1 = 1,852
A1 = 1,15
Kemudian beri nilai pada salah satu resistor untuk penguatan op-amp, contoh R7 = 1k maka R8 dapat dicari sebagai berikut :
A1 = (R7 / R8) + 1
1,15 = (1k / R8) + 1
0,15 = 1k / R8
R8 =1k / 0,15
R8=6,67k
Langkah keempat : Mendesain rangkaian high pass filter orde 4 yang ditunjukan pada Gambar 9.
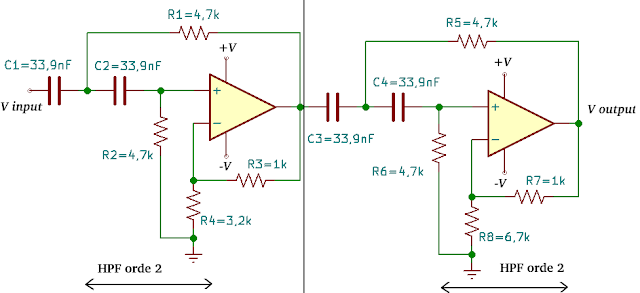 |
| Gambar 9. Rangkaian high pass filter orde 4 |
EoF